SRM 정리 - Chapter 3. Linear Regression: Standard Error, $R^2$, and $t$ statistics

Regression의 설명력을 알기 위해 다음과 같이 total deviation을 unexplained deviation과 explained deviation으로 나눌 수 있다. 즉 x에 대한 정보가 없는 deviation은 x의 정보+ x의 정보로 인해 설명되는 deviation과 같다. 

\begin{align*}
y_i - \overline{y} &= \underbrace{y_i - \hat{y}_i}_{\text{unexplained deviation}} + \underbrace{\hat{y}_i - \overline{y}}_{\text{explained deviation}} \\
\text{total deviation} &= \text{unexplained deviation} + \text{explained deviation}
\end{align*}

위의 식을 양변을 제곱하고 전체 $y_i$에 대해 더하면 다음과 같다.

$$\sum_{i=1}^{n} (y_i - \bar{y})^2 = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2$$

이때 왼쪽 식의 제곱식 안을 $y_i - \bar{y} = (y_i - \hat{y}_i) + (\hat{y}_i - \bar{y})$로 쓸 수 있으므로, 제곱식을 풀어서 쓰면 $2 \sum_{i=1}^{n} (y_i - \hat{y}_i)(\hat{y}_i - \bar{y})$식이 추가로 나온다. 이때, $2 \sum_{i=1}^{n} (y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) = 2 \sum_{i=1}^{n} \hat{\varepsilon}_i (\hat{y}_i - \bar{y})=0$이므로 이 식은 무시할 수 있으므로 위와 같은 식을 얻을 수 있다.

 

위의 식에서 첫번째 term인 $\sum_{i=1}^{n} (y_i - \bar{y})^2$ 은 total sum of squares(Total SS), 두번째 term $\sum_{i=1}^{n} (y_i - \hat{y}_i)^2$은 error sum of squares(Error SS) , 마지막 term $\sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2$은 regression sum of squares(Regression SS)이라고 한다. 이때 total SS는 regression을 하기 전에 response에 내재되어 있는 변동성을 측정한 것이고, Regression SS는 regression을 적용한 이후 남아있는 변동성을 측정한 것이다.  ISLR 교재에서는 Error sum of squares를 sum of squared residual로 RSS라고 표기하니 혼란에 주의하자.

 

이때, Total SS와 Regression SS는 각각 식을 다음과 같이 적을 수 있다.

$\text{Total SS} = \sum_{i=1}^{n} y_i^2 - n \bar{y}^2$

$\text{Regression SS} = \sum_{i=1}^{n} \hat{y}_i ^2 - n \bar{y}^2$

 

Degrees of freedom은 Total SS는 n-1, Regression SS는 k, Error SS는 n-k-1이다. 

 

chapter 3.1 Residual standard error of the regression

 

회귀분석의 정확도를 측정하는 방법으로는 residual standard error(RSE)와 $R^2$이 있다. 이 중 RSE는 $\epsilon$의 standard deviation을 추정한 것으로 response 변수가 true regression line에서 떨어진 정도의 평균을 측정한 것이다. 이를 수식으로 나타내면 다음과 같다. 

$$\text{RSE} =\sqrt{\text{MSE}}= \sqrt{\frac{1}{n - p-1} \text{Error SS}} = \sqrt{\frac{1}{n - p-1} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}$$

Regression SS는 변수를 추가할수록 감소하지만 이 감소가 $p$의 증가에 비해 작다면 더 많은 변수를 가진 모델은 더 높은 RSE를 가질 수 있다. 즉 변수가 증가할수록 모델은 복잡해지므로 이에 대한 패널티로 $p$를 부과한 것이다.

 

Chapter 3.2 $R^2$: the coefficient of determination

 

회귀분석의 정확도를 측정하는 다른 방법으로는 $R^2$가 있다. 위에서 구했던 RSE는 $Y$의 크기에 따라 값의 차이가 크다는 단점이 있으므로 $R^2$는 variance 중에 회귀로 의해 설명되는 부분의 비율을 측정하여 항상 0과 1 사이의 값을 가진다. $R^2$는 coefficient of determination(결정계수)라고 한다. 이를 수식으로 나타내면 다음과 같다. 

$$R^2 = \frac{\text{Regression SS}}{\text{Total SS}} = 1 - \frac{\text{Error SS}}{\text{Total SS}}$$

따라서 $R^2$는 $Y$의 변동성 중에서 $X$로 설명할 수 있는 부분의 비율을 측정한 것이다.

 

$R^2$와 마찬가지로 correlation 또한 $X$와 $Y$ 사이의 선형관계를 측정한다. 식은 다음과 같다.

$$\text{Cor}(X, Y) = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2 \sum_{i=1}^{n} (y_i - \bar{y})^2}}$$

Correlation은 -1과 1 사이의 값을 가지며 0보다 큰 경우에는 양의 상관관계, 0보다 작은 경우에는 음의 상관관계를 가진다고 한다. 절댓값이 클수록 상관관계가 강해진다. 상관계수는 평균, 분산의 크기 및 측정 단위에 의존하지 않기 때문에 여러개의 데이터 세트끼리 비교하기 쉽다. Simple linear regression에서는 $R^2$와 correlation 제곱 값은 같지만 multiple linear regression에서는 correlation을 사용할 수 없다. 

 

$R^2$는 직관적이지만, 변수를 추가할수록 변수와의 상관성은 관계없이 $R^2$은 증가하는 단점이 있다. 이를 해결하기 위해 adjusted $R^2$를 사용한다. 

 

Chapter 3.3 $t$ statistics

 

앞의 chapter 2에서 배웠던 standard error를 통해 계수에 대한 hypothesis test를 할 수 있다. 이때의 null hypothesis는 $X$와 $Y$ 사이에 관계가 없다는 것이고, 반대로 alternative hypothesis는 $X$와 $Y$ 사이에 어떤 관계가 있다는 것이다. 즉, basic linear regression을 가정할 때, 다음과 같은 식을 test한다. 

\begin{align*}
H_0 & : \beta_1 = 0 \\
H_a & : \beta_1 \neq 0
\end{align*}

따라서 $\beta_1$이 얼마나 0으로부터 떨어졌는지를 검증한다. 이는 $\beta_1$의 정확도와 관련이 있다. $\beta_1$이 매우 정확하다면, 0으로부터 조금만 떨어져있어도 null hypothesis를 기각할 수 있지만, 정확도가 낮다면 많이 떨어져있어야 기각할 수 있다. 따라서 정확도인 $ \text{SE}(\hat{\beta}_1) $를 이용해서 t-statistics를 계산할 수 있다.

$$t = \frac{\hat{\beta}_1 - 0}{\text{SE}(\hat{\beta}_1)}$$

Null hypothesis가 성립한다면, 위의 t-statistic이 n-2 degrees of freedom을 가지는 t분포를 따른다고 할 수 있다. 이때 t분포는 종모양의 분포로 n이 30이상으로 크다면 정규분포와 근사하다. 

위의 t statistics을 이용하여, $\beta_1=0$이라고 가정할 때, 절댓값이 t 이상인 숫자를 관찰할 확률을 p-value라고 한다. 다시 말해, p-value가 낮다면 $X$와 $Y$ 사이에 관계가 없다는 가정 하에, 우연히 이런 관계를 관찰할 가능성이 낮다, 즉 가정이 성립하지 않으므로 $X$와 $Y$에 어떤 관계가 있다.

 

Chapter 3.4 Added variable plots and partial correlation coefficients

 

변수들 간의 관계를 확인할 때, 산점도 그래프와 상관관계 표는 변수들간의 관계를 쉽게 요약한다. 하지만 변수 쌍 간의 관계만 포착할 수 있으며, 여러 변수들 간의 관계는 확인하기 어렵다. 그럼에도 불구하고 그래프는 변수들 중 분석에 유용한 변수를 판별할 수 있다는 장점이 있다.

eg.

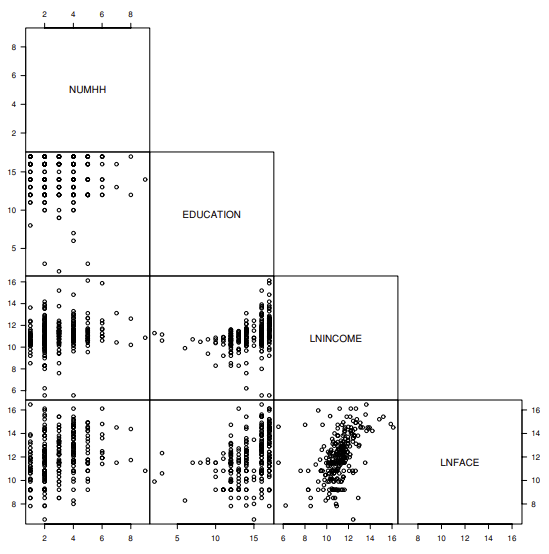
위의 그래프는 RMAF 교재의 생명보험회사 데이터로 가족구성원 수, 교육, 소득수준, 보험금에 관한 데이터이다. 위의 산점도를 통해 두 변수 쌍끼리의 관계를 파악할 수 있다. 

 

또한 추가 변수에 대한 correlation은 partial correlation coeffcient라고 하며 다음과 같이 정의된다. 

$$r(y, x_j | x_1, \ldots, x_{j-1}, x_{j+1}, \ldots, x_k) = \frac{t( \hat{\beta_j} )}{\sqrt{(t( \hat{\beta_j} ))^2 + n - (k + 1)}}.$$

이는 다른 변수들이 존재할 때 $x_j$와 $y$ 사이의 correlation으로 $ t( \hat{\beta_j} )$는 전체 regression에서 $\hat{\beta_j}$의 t-ratio이다. 위의 식을 통해 partial correlation coefficient를 계산할 때 단 하나의 회귀만 사용하는 것을 알 수 있다. 또한 t-ratio와의 관계를 이용해 빠르게 계산할 수 있지만 비선형 관계를 감지하지 못한다.